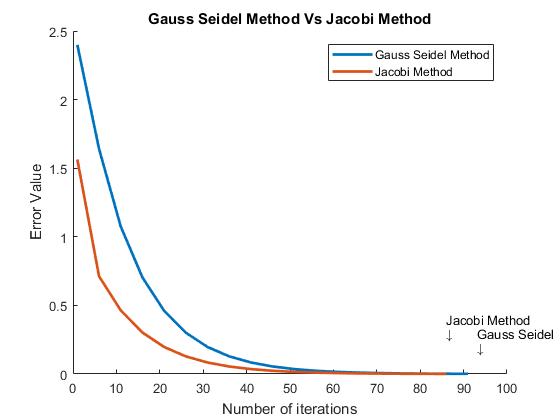
高斯塞德尔法和雅可比方法比较
雅可比方法:
雅可比(Jacobi)迭代方法是一种用于确定线性方程组的对角线主导系统解的算法。 求解每个对角线元素,并插入一个近似值。然后重复该过程,直到收敛为止。
高斯-塞德尔方法
预览截图
应用介绍
雅可比方法:
雅可比(Jacobi)迭代方法是一种用于确定线性方程组的对角线主导系统解的算法。 求解每个对角线元素,并插入一个近似值。然后重复该过程,直到收敛为止。
高斯-塞德尔方法:
高斯-赛德尔(Gauss-Seidel)方法,也称为利勃曼(Liebmann)方法或连续位移法,是一种用于求解线性方程组的迭代方法。
实现这两种算法,迭代进行了对比
©版权声明:本文内容由互联网用户自发贡献,版权归原创作者所有,本站不拥有所有权,也不承担相关法律责任。如果您发现本站中有涉嫌抄袭的内容,欢迎发送邮件至: [email protected] 进行举报,并提供相关证据,一经查实,本站将立刻删除涉嫌侵权内容。
转载请注明出处: apollocode » 高斯塞德尔法和雅可比方法比较
文件列表(部分)
| 名称 | 大小 | 修改日期 |
|---|---|---|
| GaussSeidel_Jacobi.mlx | 28.70 KB | 2017-05-24 |
| Gauss_Seidel.m | 0.76 KB | 2017-05-24 |
| Jacobi.m | 0.71 KB | 2017-05-24 |
| license.txt | 1.28 KB | 2017-05-24 |


发表评论 取消回复